西安软件测试需要学什么?软件测试的Rayleigh缺陷分析法

　　西安软件测试需要学什么?本章节主要讲解“软件测试的Rayleigh缺陷分析法”Rayleigh模型是Weibull分布系列中的一种。Weibull分布又称韦伯分布、韦氏分布或威布尔分布，由瑞典物理学家Wallodi Weibull于1939 年引进，是可靠性分析及寿命检验的理论基础。Weibull分布能被应用于很多形式，包括1参数、2参数、3参数或混合Weibull。3参数的Weibull分布由形状、尺度(范围)和位置三个参数决定。其中形状参数是最重要的参数，决定分布密度曲线的基本形状，尺度参数起放大或缩小曲线的作用，但不影响分布的形状。

　　它的累积分布函数(CDF)和概率密度函数(PDF)为：

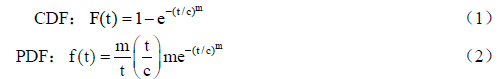
　　参数说明：m为形状参数(Shape Parameter);c为范围参数(Scale Parameter);t为时间。在软件测试过程中，一般使用概率密度函数PDF来表示缺陷密度随时间的变化情况，积累分布函数为累计缺陷分布情况，在使用Rayleigh模型分析缺陷时，形状参数m取值为2。

　　将m值代入公式(1)和公式(2)中，累积分布函数(CDF)和概率密度函数(PDF)为：

　　c参数为常量c2tm，tm是f(t)达到峰值时对应的时间。在实际应用过程中，会在公式前面乘一个系数K(K为所有的缺陷数)，将K值代入公式(3)和公式(4)中，累积分布函数(CDF)和概率密度函数(PDF)为：

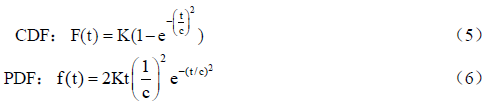
　　缺陷tm时间的比率m F(t)/K ≈0.4，即当f(t)达到最大值时，已发现的缺陷数约为总缺陷数的40%。统计测试中所发现的缺陷数，如表9-6所示。

表9-6 测试中缺陷分布

　　从表9-6中可以看出，第3周发现的缺陷数最多，截止到第3周所发现的缺陷数应该大约占全部缺陷总数的40%，则K(总缺陷数)=(前3周缺陷总数)/0.4=(20+38+55)/0.4=113/0.4=282。tm等于3，那么c?2tm?32 。将K值和c值代入公式(5)和公式(6)中，累积分布函数(CDF)和概率密度函数(PDF)为：

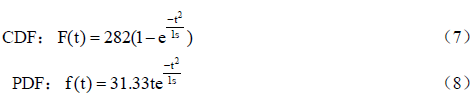
　　使用Rayleigh 模型生成的模拟值见表9-7。

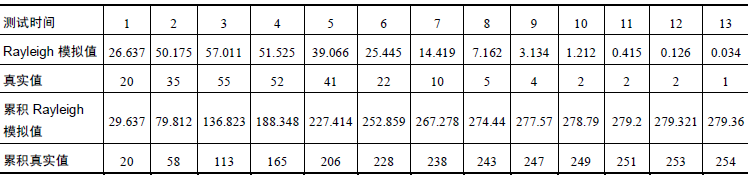
表9-7 真实缺陷数与Rayleigh 模拟缺陷数

　　累积分布函数(CDF)与真实数据图如图9-23所示。

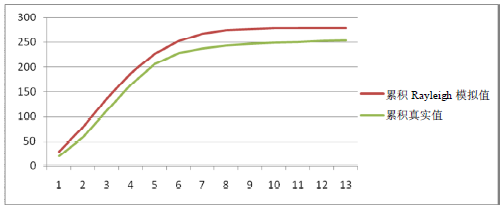
　　图9-23 累积分布函数(CDF)与真实数据图

　　概率密度函数(PDF)与真实数据图如图9-24所示。

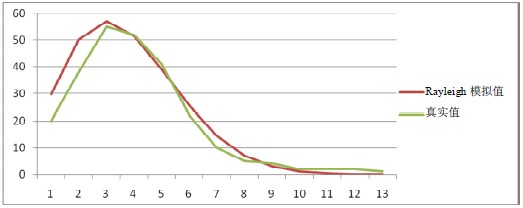
　　图9-24概率密度函数(PDF)与真实数据图

　　【实例】通过Rayleigh模型的概率密度来评估测试过程和软件质量。计划升级一个历史项目，以前的历史数据统计表明，该项目千行代码缺陷率为9.56 个，估计升级后该项目的代码行数为102KLOC(千行)，希望本次升级发现的千行缺陷数比之前少5.3%，即总缺陷数预计为9.56×102×(1-5.3%)=923.44 个，计划项目的测试时间为22 周。将数据代入到Rayleigh 模型中的概率密度函数中，得到PDF 为：

　　使用Rayleigh 模型生成的模拟值见表9-8。　　

表9-8Rayleigh 模拟值

　　使用Rayleigh模型生成概率密度函数图，如图9-25所示。

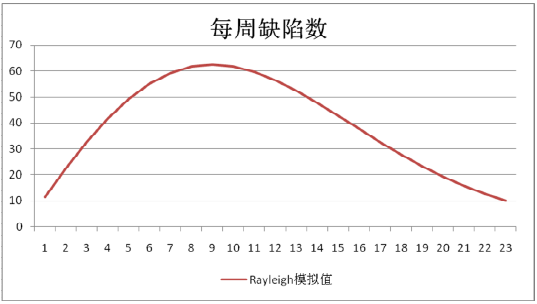
　　图9-25 概率密度函数(PDF)图

　　测试过程应该将该图与测试过程真实的每周发现的缺陷数进行对比，如果两个图存在明显的差异，那么说明测试策略存在问题，需要重新修改测试策略。